Logistic Regression is a Supervised Machine Learning Algorithm use for the classification problem. Now, you might wonder how regression can be use for classification problem.
The reason is; it works on the principle of Simple Linear Regression. Logistic Regression is taken from the field of statistics, where it is used to categorize the classes into true or false, spam or not spam etc.
The Logistic Regression uses a more complex cost function than the Linear Regression, the cost function used is Sigmoid Function or Logistic Function.
Sigmoid Function
Sigmoid Function gives the output in the range of (0, 1) and mathematically represented as :

The Sigmoid Function gives an ‘S’ shaped curve. S(x) is output between 0 and 1, where ‘x’ is an input to the function
This curve has a finite limit of:
‘0’ as value(x) approaches −∞
‘1’ as value(x) approaches +∞
def sigmoid(x):
return 1 / (1 + np.exp(-x))
Here, our function will return probabilistic value between 0 and 1. But what if we want discrete class like (spam / not spam), then we have to set threshold value.
Let’s take an example to understand:
Supposed you have dataset of 10,000 dog images and you train your model on that dataset. Now, you have given a job to classify cat and dog from a dataset of 1 million images , and you want to use same model that you had train on dog dataset. So, you set the threshold value to 0.5, and mentioned if the predicted value is above 0.5; it’s a dog class and below 0.5 it’s a cat class. In this way you can classify 1 million images into two classes.
Error Calculations
In logistic regression the sigmoid function is non-linear. Squaring of this function will result into concave function with many local minimums. So, gradient decent will find difficulties to get global minimum. So, MSE is not a option here to calculate cost.
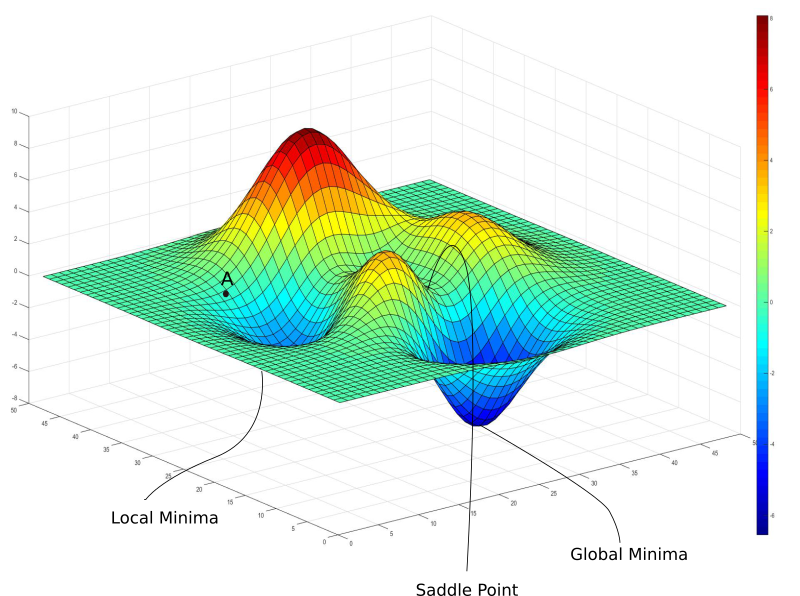
To calculate error or cost we mainly use the log-loss function. It is given as follows with respect to particular attribute and probability :

cost = (1/m)*(((-y).T @ np.log(h + epsilon))-((1-y).T @ np.log(1-h + epsilon)))
- y = output variable
- h = sigmoid function
Log–loss is an appropriate performance measure when you’re model output is the probability of a binary outcome.
To minimize the cost, we can use gradient descent just like we used in Linear Regression.

Leave a Reply